g) Making Runge and Mara Figure 28.5
Nathan L. Brouwer
2022-03-07
h-make_figure_28_5.RmdIntroduction
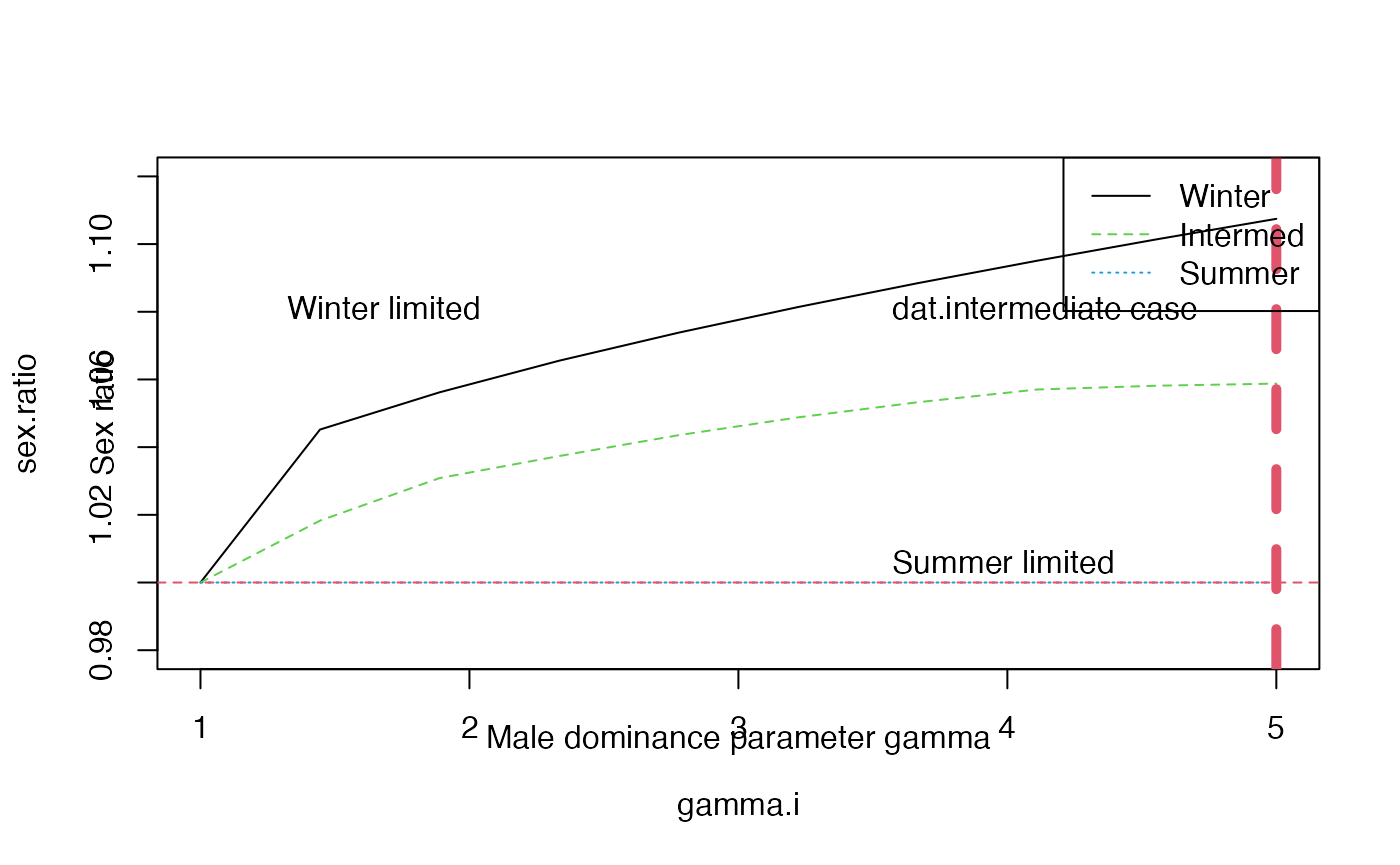
Figure 28.5 investigates how changes in the male dominance parameter (gamma) impacts the sex ratio in the context of three scenarios
- A winter limited population (K.bc = 800 pair, K.wg = 485 individuals)
- A breeding season (summer) limited population (K.bc = 205, K.wg = 580)
- An intermediate scenario (K.bc = 205, K.wg = 900)
Making Figure 28.5 the easy way
Load the package
library(redstart)There param_ranges() function has a “figure = …” arguement and also a “scenario = …”.
The intial range of the parameters are made by setting “figure = 28.5” and “scenario” to “winter”, “summer”, or “int”. This sets the fixed parameters for each value and the min of gamma to 1 and the max of gamma to 5.
F28.5.range.winter <- param_ranges(figure = 28.5, scenario = "winter")
#> Setting breeding 'source' carrying capacity K.bc to 800
#> Setting winter 'good' carrying capacity K.wg to 484
#>
#> Setting male winter dominance parameter to vary from 1 to 5
F28.5.range.summer <- param_ranges(figure = 28.5, scenario = "summer")
#> Setting breeding 'source' carrying capacity K.bc to 205
#> Setting winter 'good' carrying capacity K.wg to 900
#>
#> Setting male winter dominance parameter to vary from 1 to 5
F28.5.range.inter <- param_ranges(figure = 28.5, scenario = "int")
#> Setting breeding 'source' carrying capacity K.bc to 224
#> Setting winter 'good' carrying capacity K.wg to 580
#>
#> Setting male winter dominance parameter to vary from 1 to 5This code makes a dataframe which summaries these parameters.
data.frame(winter = head(F28.5.range.winter),
int = head(F28.5.range.inter),
summer = head(F28.5.range.summer))
#> winter.min winter.max int.min int.max summer.min summer.max
#> gamma 1.0 5.0 1.0 5.0 1.0 5.0
#> co. 1.0 1.0 1.0 1.0 1.0 1.0
#> K.bc 800.0 800.0 224.0 224.0 205.0 205.0
#> K.bk 10000.0 10000.0 10000.0 10000.0 10000.0 10000.0
#> K.wg 485.0 485.0 580.0 580.0 900.0 900.0
#> S.w.mg 0.8 0.8 0.8 0.8 0.8 0.8param_seqs() generates values between the minimum and the maxium.
F28.5.win.seq <- param_seqs(F28.5.range.winter)
F28.5.int.seq <- param_seqs(F28.5.range.inter)
F28.5.sum.seq <- param_seqs(F28.5.range.summer,len.out= 20)For Figure 28.5 only the breeding ground carrying capacity is varied.
head(F28.5.win.seq,3)
#> $gamma
#> [1] 1.000000 1.444444 1.888889 2.333333 2.777778 3.222222 3.666667 4.111111
#> [9] 4.555556 5.000000
#>
#> $co.
#> [1] 1
#>
#> $K.bc
#> [1] 800All combinations of parameters are created using param_grid()
F28.5.win.grid <- param_grid(param.seqs = F28.5.win.seq)
#> The dimension of the fully expanded dataframe is:
#> 10 by 30
F28.5.int.grid <- param_grid(param.seqs = F28.5.int.seq)
#> The dimension of the fully expanded dataframe is:
#> 10 by 30
F28.5.sum.grid <- param_grid(param.seqs = F28.5.sum.seq)
#> The dimension of the fully expanded dataframe is:
#> 20 by 30Finally runFAC_multi() is called for each scenario’s grid.
F28.5.FAC.win <- runFAC_multi(param.grid = F28.5.win.grid)
#>
#> Model at equilibrium after 62 iterations
#>
#> Model at equilibrium after 156 iterations
#>
#> Model at equilibrium after 155 iterations
#>
#> Model at equilibrium after 165 iterations
#>
#> Model at equilibrium after 156 iterations
#>
#> Model at equilibrium after 156 iterations
#>
#> Model at equilibrium after 153 iterations
#>
#> Model at equilibrium after 159 iterations
#>
#> Model at equilibrium after 154 iterations
#>
#> Model at equilibrium after 149 iterations
F28.5.FAC.int <- runFAC_multi(param.grid = F28.5.int.grid)
#>
#> Model at equilibrium after 64 iterations
#>
#> Model at equilibrium after 78 iterations
#>
#> Model at equilibrium after 79 iterations
#>
#> Model at equilibrium after 82 iterations
#>
#> Model at equilibrium after 82 iterations
#>
#> Model at equilibrium after 82 iterations
#>
#> Model at equilibrium after 83 iterations
#>
#> Model at equilibrium after 83 iterations
#>
#> Model at equilibrium after 83 iterations
#>
#> Model at equilibrium after 83 iterations
F28.5.FAC.sum <- runFAC_multi(param.grid = F28.5.sum.grid)
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterations
#>
#> Model at equilibrium after 94 iterationsOnce all calls to runFAC_mulit() are done we can plot using plot_Fig28_5().
plot_Fig28_5(dat.winter.lim = F28.5.FAC.win$multiFAC.out.df.RM,
dat.intermediate = F28.5.FAC.int$multiFAC.out.df.RM,
dat.summer.lim = F28.5.FAC.sum$multiFAC.out.df.RM,
drain = T)