Chapter 19 Data analysis encounter: T-test

Nathan Brouwer, Phd brouwern at gmail.com https://github.com/brouwern Twitter lobrowR

19.0.1 Preliminaries

19.0.1.1 Load packages

library(wildlifeR)
library(ggplot2)
library(cowplot)
library(ggpubr)
library(dplyr)

19.0.1.2 Load data

data(frogarms)

19.0.1.3 Subset your data

The function make_my_data2L() will extract out a random subset of the data. Change “my.code” to your school email address, minus the “(???)” or whatever your affiliation is.

my.frogs <- make_my_data2L(dat = frogarms, 
                           my.code = "nlb24", # <=  change this!
                           cat.var = "sex",
                           n.sample = 20, 
                           with.rep = FALSE)

t-test used to tell if 2 groups are different

19.0.2 T-test

Use the t.test() function. The reponse variable (aka the y variable) is mass and goes to the left of the ~. The predictor variable (x-variable) goes on teh right. The arguement data = … is used to tell the function where the response and predictor columns are found.

This spits out R’s standard t.test table

Save to object

mass.t <-  t.test(mass ~ sex, data = my.frogs)

---

19.0.3 Optional: cleaning up output with broom() [O]

This section is optional

look at w/broom::glance. re-labels things a bit odd and would be nice to round. will stick with original R output

library(broom)
glance(mass.t)

End optional section

---

mass.t

Check the means using dplyr

my.frogs %>% group_by(sex) %>% summarize(mean.mass = mean(mass))

What does all of this mean?

Quiz

p = p interpretation = df = why df fractional? (this one is hard!) t = What would happen to p if t was bigger? What is a “95% CI” What is this a 95% CI for?

What does the CI mean?

plot_t_test_ES(mass.t)

Make a plot of the means with error bars. Save to an object called gg.means

gg.means <-ggerrorplot(data = my.frogs,
          y = "mass",
          x = "sex",
          desc_stat = "mean_ci") +
  ggtitle("Group means & error bars")

Save effect size

gg.ES <-plot_t_test_ES(mass.t) +
  ggtitle("__________ & errorbars")

Plot both

plot_grid(gg.means,gg.ES)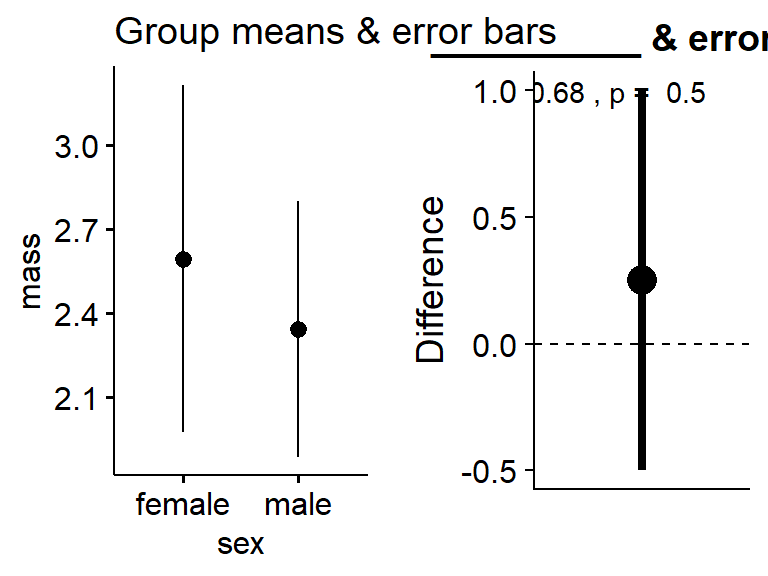

A hint

gg.means <-ggerrorplot(data = my.frogs,
          y = "mass",
          x = "sex",
          desc_stat = "mean_ci") +
  ylab("Mass (g)") +
  xlab("Sex") +
  ggtitle("Group means & error bars")


gg.ES <-plot_t_test_ES(mass.t) +
  ylab("Difference between groups (g)") +
  ggtitle("__________ & errorbars")

plot_grid(gg.means,gg.ES)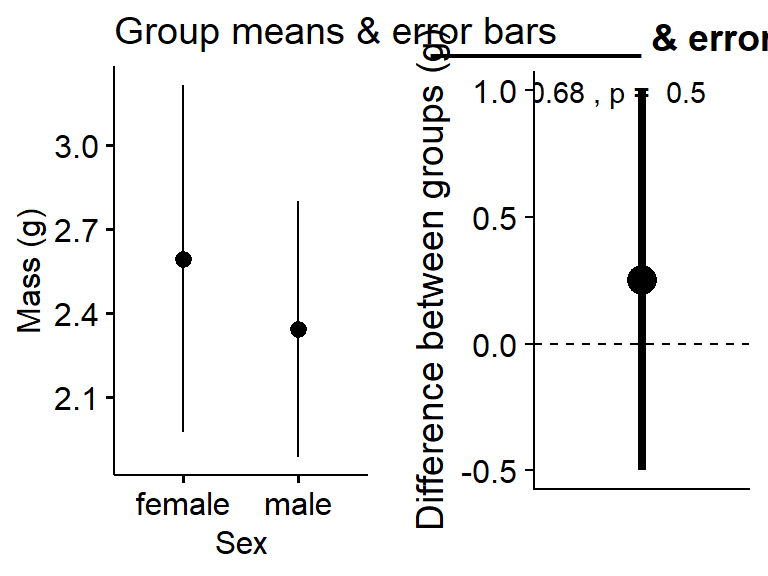

Did anyone get a significant result?

19.0.4 Arm girth

(do same thing for arm girth. see the super significant values?)

Now we are going to unpack this

---

19.0.5 Optional

This section is optional

There is a major flaw in this analysis. consider the following graph where the mass is plotted on the x-axis and the arm girth is plotted on the y-axis. Does arm girth vary just because of sex, or because of sex and mass?

This is ANCOVA. Sometimes taught as an extension of ANOVA, or as a type of regression.

ggscatter(data = frogarms,
          y = "arm",
          x = "mass",
          color = "sex")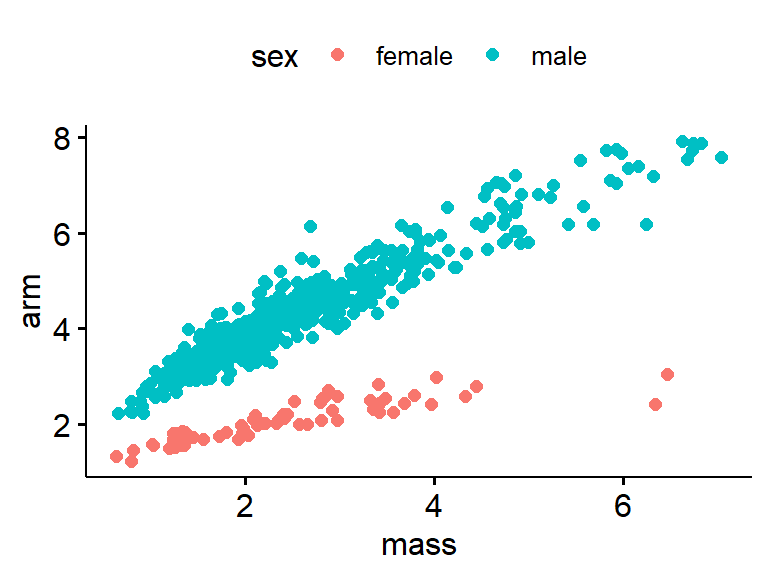

End optional section

---